詭弁論理学

目次

　はしがき

　Ⅰ　議論の種々相　1
議論べたの悩み　／　無理押しの強み　／　論弁と強弁　／　論理のあそび

　Ⅱ　強弁術　17
強弁術の誕生　18　　　権力と強弁　／　伝説の効用　／　泣く子と強弁　／　買物論争

小児型強弁　26　　　小児病　／　やむをえぬ押し　／　小児病の原因　／　無神経時代

二分法　33　　　二分法とは　／　魔女狩りの背景　／　魔女狩りの実態　／　現代の魔女狩り　／　二分法への反撃　／　ルターの場合

相殺法　46　　　相殺法とは　／　公平の原則　／　強弁補強術　／　ささやかな抵抗

強弁術の総括　55　　　強弁と常識　／　強弁と人柄

　Ⅲ　詭弁術　61
詭弁術の誕生　62　　　科学と詭弁　／　すべてが幻　／　詭弁と実利　／　東洋の詭弁　／　日本の詭弁

強弁との境　69　　　二分法　／　相殺法　／　目には目を！

あてにならない話　74　　　うがった見方　／　悪魔にもわからない　／　深遠な言葉　／　深遠な冗談

論点のすりかえ　80　　　議論のはずみ　／　上手にはぐらかす　／　感情に訴える

主張の言いかえ　85　　　正しい言いかえ　／　逆は必ずしも真ならず　／　部分より全体に及ぼす誤り　／　全体より部分に及ぼす誤り　／　三段論法　／　否定二前提の虚偽　／　不当肯定の虚偽　／　特称二前提の虚偽　／　媒概念曖昧の虚偽　／　四個概念の虚偽　／　包むということ　／　三段論法のパズル　／　三段論法の複合形　／　両刀論法

消去法　112　　　犯人さがし　／　パズルヘの応用　／　消去法の失敗　／　失敗の逆用　／　派閥の消去法　／　選言的三段論法

ドミノ理論　122　　　将棋だおし　／　身近な実例

論弁術の総括　125　　　健全な常識　／　言葉の意味　／　数字にダマされるな　／　数字をバカにするな　／　正しい議論のための原則

　Ⅳ　論理のあそび　135
やさしいパズル　136　　　初級問題解答　／　中級問題解答　／　ニューヨークでの実話

説得ということ　143　　　聞く耳もたぬ　／　ホンネとタテマエ？　／　つまずきの石　／　相手に話させる

上級パズル　148　　　ケネディの問題　／　スターリン登場

四十人の貴族とその従者　155　　　問題　／　早トチリ型　／　貴族の推理　／　議論か始まる　／　説得をめざして　／　最後のツメ

理髪師のパラドックス　166　　　どこが矛盾か　／　矛盾ということ　／　共和党論争　／　キャロルのトリック

自己矛盾を利用したパラドックス　177　　　文の正しさ　／　自分自身に言及する文　／　論理方程式　／　人食いワニのパラドックス

死刑囚のパラドックス　191　　　問題　／　問題のヴァリエーション　／　天文学博士の解答　／　パラドックスの発生　／　さまざまの見解　／　サルタンと馬　／　私の解答　／　おわりに

　〈付録〉鏡をめぐっての会話　212

　解答　223

　参考文献　225 　

はしがき

　世の中には、「話上手」な人がいて、ちょっとした集まりなどでも、その場の雰囲気を和やかにし、皆を楽しませてくれる。本書の挿絵をおひきうけくださった安野光雅画伯も、その道の達人なので、安野さんが現われただけで、皆の頬はゆるみ、横隔膜はふるえだしてしまう。私も、安野さんのために笑いすぎて、涙をこぼしたことが何度あったろうか。
　一方世の中には「議論上手」な人がいて、これはあまり人に好かれないようである。「議論べた」はいつも、あとになってから「ああ、あのときはこういってやればよかった」と後悔する。私はいつも後悔ばかりしているので、しまいには「後悔する」ことを後悔するようになった。
　「後悔しない」ためには、自分が議論上手になればよい。しかしそれには、努力ばかりでなく天分も必要なので、「なろう」と思ってなれるものでもないらしい。ではどうしたらよいか。たとえ議論には勝てないとしても、冷静に、相手の戦術を分析し、人間研究の材料として利用することはできるであろう。また、時間に追われずにマイペースで、のんびり「論理のパズル」を楽しむことも悪くないであろう。なまじ「議論上手」になって人に嫌われるよりは、天分を生かして「話上手」になるか、あるいは「勝てなくてもよい」という前提で議論を楽しむ「ゆとり」を身につけたほうが、はるかに好ましいのではないかと思う。この「ゆとり」を望む人々（私自身を含む）のために、本書は生まれた。
　本書が所期の目的にかなっているかどうか、もとより私にはわからないが、ただ強弁をふるうための「ハウツーもの」として利用されないことだけは、著者として希望している。
　詭弁論理「学」というたいへんな書名をつけてしまったのも（ハウツー式に「議論の術を身につける」ものではない、という意味で）知的・論理的な観察が主体であることを、強調したいためであった。別に（記号）論理学の知識を要求するわけでも、教えようとするわけでもないから、書名におそれをなした方でも、せめてⅠ章を眺めてから「むずかしいかどうか」の判断をつけてくださるよう、お願いしたい。
　本書の企画・出版に際して、中央公論社の加納信雄さんにたいへんお世話になった。相性のいい編集者を得て、ひさしぶりに楽しい仕事ができたことを、厚くお礼申しあげたい。
　　　　　 1976年9月25日

論理のあそび

　ところで「頭は悪くないつもりだが、どうも議論は苦手だ」という人におすすめしたい、気分転換法がある。それは、論理のあそび（「言葉のパズル」）といってもよい）である。ひとつ簡単な例をお目にかけよう。
　さる貴婦人が、みごとな指輪を、一万ドル払って買った。ところがその貴婦人は、翌日同じ店にやってきて、「昨日の指輪は気に入らないから」と、二万ドルの指輪ととりかえて立ち去ろうとした。店員が驚いて、差額の一万ドルを求めたところ、その貴婦人も驚いてこういった。
　「きのう私はあなたに一万ドルを払ったでしょう？　今日またこうして、一万ドルの値打ち の指輪を返しだのだから、あわせて二万ドルになるじゃないの」
　この貴婦人に納得してもらうために、店員はどんなふうに説明すればよいであろうか？
　あまりにもバカバカしいできごとで、かえって返事がむずかしそうである。模範解答というつもりではないが、思いつく解答をいくつか挙げてみよう。
　「それは困ります。あと一万ドルお払いください」
　これでは説明にも説得にもならない。押し問答である。とっさの場合には、こんな答しか出てこないかもしれないが、今は「あそび」で考えているのだから、もう少しじっくり考えてみよう。
　「失礼ですが、お客様はどちらの小学校をご卒業ですか？」
　これは先制攻撃法としては悪くないかもしれない。しかしこれもやはり説明とはいえない。
　「きのうのお取引は、きのうですんでおります。今日またお買物をしていただけるなら、あらためてお金を頂戴しなければなりません」
　これもまだ、あまりエレガントとは思えない。相手のまちがいをヒンヤリとやっつけているので、かえってわかりにくく、押し問答にもどってしまう危険がある。そこで、相手の考えにあわせて説明する仕方を工夫してみよう。
　「奥様、でも私どもは、昨日奥様に一万ドルの指輪をさしあげております。今日また二万ドルの指輪をさしあげますと、あわせて三万ドルになってしまいます」
　「あら、昨日の指輪は、さっき返したじゃないの」
　「ええ、でもその指輪のことは帳消しといたしますと、私どもはまだ一万ドルしかいただいておりません」
　これでわかってもらえなければ、「小学校」をもちだして追っぱらうか、こちらもネバって押し問答に入る覚悟を固めなければならない。もちろん「あそび」の場合にそういう心配はないから、「オマワリサーン」とか「ご主人様にお電話させていただきます」など、おもしろ半分のセリフもいろいろ考えてみればよい。

　＜中略＞

　もっと軽いパズルか好きな方は、次の問題のどれかに挑戦していただきたい。

　【初級問題】
　個室が十二部屋しかない小さなホテルに、十三人の客がやってきた。何とかみんな泊めてしまおうと頭をひねったマネージャーは、まず最後についた客に、かりに（一時的に）１号室に入ってもらい、それからほかの客を、その１号室からはじめて各部屋にひとりずつ、順番に割り当てていった。
　こうして１号室だけは、ふたりが入った。そして三番めの人は2号室に、四番目の人は3号室に、五番めの人は4号室に入った。以下、六番めの人は5号室に、……と続いて、十二番めの人が11号室に入った。
　それからマネージャーは、あいている12号室に、さっき１号室に入ってもらった「最後の客」をつれてきた。これでめでたく、十三人の客が十二の個室に、ひとりずつ泊れたことになる。
　どこがまちかっているか？

　【中級問題】
　買物上手のＡ君に、Ｂ、Ｃ、Ｄの三人か千円ずつ出して、三千円のレコードを買うのを依頼した。Ａ君は五百円だけ値切って買い、二百円を着服して、残り三百円とレコードを三人に渡した。三人は喜んで、おつりを百円ずつわけた。
　さて、Ｂ、Ｃ、Ｄは一人九百円ずつ出したことになるので、三人の出費はあわせて二千七百円である。これにＡ君か着服した二百円を加えると二千九百円になり、最初の三千円より百円少ない。
　不足の百円は、どこに消えたのだろうか？

＜以下略＞
 

小児病

 　これまでたびたびとりあげてきた、寅さんや子供がふりまわす強弁は、相手がいうことを耳に入れず、ひたすら「自分がいいたいことをいいつのる」という点に特徴かある。これを、小児型の強弁と呼ぶことにしよう。それしかできない寅さんのような人は、小児病と呼べばよい。軽度の小児病患者は頭脳優秀な青年にもよく見られるので、私の経験でも次のようなことがあった。
　ある負けずぎらいの大学生と、東京の私鉄（京王線）の特急電車に乗ったときに、次の停車駅まで何分かかるかが話題になった。途中とばされる駅の数は車内の掲示でわかったので、その大学生（かりにＳ君とする）は、ひとつの駅あたりおよそ二分半とみて、所要時間を計算した。私は大体の所要時間を知っていたから、そこから逆算して、ひとつの駅あたりでは二分もかからないと主張した。
　私は手をかえ品をかえ、「この前乗ったときは……」とか「この線は駅の間隔が短いから……」などといってみたのだが、Ｓ君の返事はいつも同じだった。
　「いやあ、二分以上はかかりますよ」一言一句変らないところが、絶対の自信をあらわしていて、腹立たしいやらおかしいやら、まあ優等生というものはこういうものかな、と思っていると、やがて電車は次の停車駅（調布）についた。そこで一駅あたりの平均所要時間を計算してみると、果たせるかな、一分五十秒と出た。そこで、私か相手をなぐさめるつもりで「だいたい二分でしたね」といったところ、Ｓ君の返事がふるっている。
　「いやあ、平均一分五十秒でしたよ」 彼の顔は、つねに自信にみちていた。
　ここで、久君と正君の「あーるもん」「なーいもん」論争を連想された方もおられるであろう。途中で意見がころころ変っても、各瞬間では、正君もＳ君もつねに勝利者（少なくとも、負け知らず）であった。正君のほうはまだしも、「二階だての自動車は、今はないが、作ることはできる」と解釈してやれば、（事実には反するが）前後の辻棲はあうけれども、優秀な大学生であるＳ君は、全くの自己矛盾に陥っている。こんなふうに、つねに相手を押えようとするタイプの小児病患者には、それなりの強さがあると同時に、前後の一貫性がおろそかになるため、冷静な観察者にはどうしてもボロを出しやすい一面がある。

二分法

 　権力者や組織の有能な指導者たちは、思いついたことをただいいたてるような、単純な強弁術は使わない。もう少し詭弁術に近い、しかし精神的・肉体的・経済的その他もろもろの威嚇を伴う、有効な技術を駆使する。そのひとつがここでとりあげる二分法である。

　二分法とは
　人々や考え方などを、ある原理的な基準でふたつに分けてしまう考え方を、二分法という。テレビっ子ならすべての人間を「ワルモノ」と「イイモノ（善人）」に分けるであろう（イギリスの子供は、昔の王さまの話が出るとすぐ、「それ、いい王様？　悪い王様？」ときくという）。このように分けるのは、話を簡単にするためには便利であるが、善と悪の谷間にさまよう凡人たちを十把ひとからげにして悪人扱いにしてしまうと、いろいろ問題か出てくる。
　たとえばここに、悪を憎むスーパー・ロボットが誕生したとしよう。そのロボットが、一回でも悪いことをしたことがある人間を、みな殺しにするとしたら、世の中はどうなるであろうか？　また、殺さないまでも、「一度でも過ちを犯したものは罪人だ。だから私のいうことに従わなければならない」として、奴隷的な労働を強制するとしたら、どうであろうか？　そのロボットは、よいことも悪いこともするという人間の実情を無視して、二分法を乱用したことになる。世の中はまっ暗、そこでテーマ・ソングにのって、鉄腕アトムかグレートマジンガーが登場する……。
　強大な権力をもって二分法をおし通した極端な実例は、中世ヨーロッパにみられる。教会による「魔女狩り」がそれである。これには二分法の性格がよくあらわれていると思うので、少し詳しく観察してみよう。

強弁と常識

　強弁術の要諦を格言ふうにまとめると、次のようになるであろう。
　(1)　相手のいうことを聞くな。
　(2)　自分の主張に確信を持て。
　(3)　逆らうものは悪魔である（レッテルを利用せよ）。
　(4)　自分のいいたいことは繰り返せ。
　(5)　おどし、泣き、またはしゃべりまくること。
　このようなワザの達人を、はびこらせてはならない。といっても、小児型強弁術について前に観察したように、根が深いところにある（らしい）ので、なかなか絶滅はむずかしかろうと思う。ただ、常識がないために自分の感情をふりまわす「悪気のない強弁術者」に対しては、健全な常識を作りあげ、普及させることが有益であろう。
　よい例が、交通法規の発達である。みんなが安全運転を心がけ、常識に従って車を運転すれば、事故などやたらに起らないはずであるが、実は「常識」というものが案外アテにならないので、六割の人か常識と思っていることでも、あと四割の人は知らなかったり、反対に考えたりするものなのである。そこで、「細い道から広い道に出るときは、広い道のほうの通行をさまたげないようにすること」とか「同じぐらいの広さの道が交差しているところで、二台の車が同時に交差点にさしかかったときは、左側の車のほうが優先的に通行できる」などというふうに法律できめて、共通の常識をいわば「作りあげて」ゆくのである。
　団地での騒音公害についても、しだいに詳しい常識を作りあげなげればならない。たとえばトイレの水音や赤ん坊の泣き声などの「生活音」と、ピアノの音や室内でのハイヒールの足音などの「騒音」を区別することか第一歩である。また、許される騒音の程度 ―― 音量や時間帯などの目安がきまってくるとよい。日本で適当かどうかわからないが、フランスでは「午後八時」という目安かあり、アパートでそれより遅くピアノをひいていると、警察に電話されても文句はいえない。
　脱線ではあるか、建物の出入ロでのマナーは、何とかならないものだろうか。ヨーロッパでは、自動車の運転マナーは（イギリスを除いて）あまりよいともいえないけれど、人と人とが出入口や曲り角などでぶつかりそうになったときは、ともかく「相手に譲る」こと、急ぐほうや譲られたほうが「ありがとう」とか「すみません」と声をかけることは、常識としてよく普及している。日本では、「ともかくすりぬけて前進する」というのが常識で、デパートや地下鉄など混雑するところはもちろん仕方がないけれども、何でもない出入口や道路でもその「常識」が発揮される。すいている道で人と人とがすれちがうときにも、お互いに譲りあう習慣がないものだから、最後の瞬間に最小限の動作で、肩をふれあわんばかりにしてすれちがっていく。これも、日本在住の外国人にとっては、相当にうす気味悪いものであるにちがいない。

論点のすりかえ

　　　議論のはずみ
　もののはずみで、議論が横道にそれてしまうのはよくあることである。ごく軽い例として、また寅さんに登場していただこう。ご存じ「男はつらいよ」葛飾立志篇で、学問を志したフーテンの寅さんか、眼鏡をかけて町内をうろつきはじめた。
　博「いいですか、勉強をして眼が悪くなって、その結果、眼鏡をかけるんですよ。眼鏡をかけたからって勉強したことにはなりませんよ」
　寅「気分だといっているんだ、気分から入るんだからさ。ね、新しい褌をつければ体だってキリッとするじゃないか」
　博「今、褌の話してんじゃありませんよ、眼鏡の話しているんですよ」
　寅「たとえ話よ。お前だってそういうことかあるだろ、新しい褌したら、その気持になるんじゃないか」
　博「僕はパンツですよ」
　寅「あ、そうか、お前パンツか。お前のようなパンツ野郎とは話合いにならないよ」
　博「パンツはいてどこが悪いんですか」
　眼鏡論争からパンツ論争へ、はずみというものはおそろしい。しかしこれは必ずしも偶然的なはずみではなく、寅さんのほうから「仕掛けた」はずみである。詭弁家にとっては、こういう「仕掛け方」が参考になると思うが、われわれとしては、へんなはずみを作らないよう、「仕掛けにのるな」という教訓を得たことにしておきたい。

　　　上手にはぐらかす
　論点をすりかえて、相手の追及をはぐらかすことも、ユーモアの域に達すると、法廷の場においてさえ、第三者の共感をかちうることがある。
　イギリスの偉大な法律家で、のちに王室裁判所長になったクールリッジにも、素人の証人にしてやられた経験がある。彼は、規則を守らないからと退学になった少女のために、学校側を名誉毀損で訴えた。クールリッジは、学校側の証人ミセス・ケネディに、退学させられた少女のどこか悪かったのかとつめよった。するとケネディ夫人は、少女が「いちごを食べた」という例を挙げた。
　クールリッジ「へえ、いちごを食べたのですか。どうしてそれが悪いのですか」
　ケネディ夫人「禁じられておりました」
　「しかし、いちごを食べるとどんな厄介なことか起るのですか」
　「どうか、りんごを食べるとどんな厄介なことが起るのか、きいて下さいませ。ご存じの通り厄介なことが起っています」
　この「りんご」はもちろん、アダムとイヴが食べて「裸であることを知り、いちじくの葉をつづり合わせて、腰に巻いた」うえ、エデンの園から追いだされたという、「善悪を知る木」の実をさしている。法廷の全員が爆笑し、クールリッジでさえ、椅子にひっくりかえって笑った。この裁判は結局取下げになったという（戒能通孝、前掲書）。

　　　感情に訴える
　日本の法廷ではどうなのだろうか。陪審制ではないからか、あまりおもしろい話はきいたことがないけれども、すぐ思いだされるのは外務省秘密漏洩事件である。
　この事件のポイントは、「報道の自由」の解釈と、蓮見事務官から西山記者に手渡されたいわゆる「秘密」なるものが、どの程度の秘密だったのか、ということである。ところが起訴状の中に「情を通じ」などという古い言葉があって、ジャーナリズムがとびついたために、世間の受けとめ方はかなり感情的になってしまった。それが検察側のねらいだったのかどうかは知らないが、西山記者の評判は落ち、「太吉だなんて、名前からして太い野郎だ」と息まく人まであらわれる始末である。これは近来稀にみる、みごとな「論点のすりかえ」である。
　私は、（学生にいわせれば）頭が古いほうだから、女性を手玉にとることが許されるとは少しも思っていない。しかし、検察側か指摘している事柄は、「手玉にとる」とか男女関係をタネに「脅迫した」ということではなくて、単に「男女関係があった」ということだけである。「男女関係があったから悪い」というけれども、男女関係ぬきのスクープならさしつかえなかったのだろうか。余計なことはいわずに、「秘密を漏らさせたのが悪い」一本槍で押したほうか、論理的にはるかに明快である。憲法に保障されている報道の自由との関係で、裁判所は別の判断を示すかもしれないが、それはまたそのときに控訴するかどうか考えればよい（ついでながら、姦通罪を罰する法律は、昭和22年の刑法改正で廃止されている）。
　もうひとつ、私が全く理解に苦しむのは、二審（控訴審）の判決である。検察側の主張も弁護側の主張も（賛成という意味ではないが）一応理解できるし、一審判決も（少なくとも論理的に）きわめて明快であるが、二審の判決文はわからないことだらけである。これでは弁護側か納得できないのはもちろん、検察側としても困るのではなかろうか？
　第一の問題点は、「秘密」の定義か曖昧なことである。秘密を漏らしたのなら刑罰を加えなければならないので、「では（国家公務員法でいう）秘密とはなんでしょう」ときくと、「刑罰で保護するに価する実質的な秘密と解される」とくる。これではまるで落語である。
　「八の家ァ、どこだね？」
　「熊五郎の家の筋向かいだよ」
　「じゃ熊五郎の家は？」
　「八の家の筋向かいだよ」
　一審判決のように「漏れても協定は調印されたのだから、実質的な秘密性はそれほど高くない」という具体的な判断にくらべて、はなはだ不明瞭である。
　第二の問題点は、「そそのかし」の定義である。「相手の自由な意思決定を不可能にする程度の手段方法または自由な意思決定のできない状態を利用してなされる行為」というくどい説明があるが、金銭で釣られて「よし、いっちょうやったるか」と積極的に秘密を漏らしたときには、「そそのかし」にならないのであろうか？　それに、男女関係がある場合でも姻戚関係がある場合でも、立派な大人の行動が、泣く泣くやったのかむしろすすんでやったのか、微妙な場合に第三者に判断できるのだろうか？　「悪魔にもわからない」ことを判断なさろうとする裁判官殿は、たぶん恋をされたことがないにちがいない。
　少々話が脱線しすぎたかもしれないか、「定義を曖昧にして、結論を簡潔に、関係ないことを長々と述べよ」というのも詭弁術のひとつであるから、この二審判決は大いに参考になることと思う。

ドミノ理論

　　　将棋だおし
　将棋の駒を机に立たせて、適当な間隔で並べてから、一番端の駒を倒すと、次々とぶつかりあって、全部の駒がきれいに倒れる。小さな子供が喜ぶ「将棋だおし」である。西洋ではこれを、「ドミノ」ゲームの札で遊ぶらしい。
　このように「ひとつが倒れれば、全部が倒れる」という理屈を、ドミノ理論という。丈夫な堤防も小さな蟻の穴から崩れるというから、これは非常に用心深い考え方であるといえる。しかしこれもあまり乱用されると、考え方や行動が窮屈になり、自由で適切な判断ができなくなって「硬直化した」などといわれる破目になる。アメリカが南ベトナム政権にあれほどこだわったのも、ドミノ理論のためである。ソ連がチェコの自由化を許さなかったのも、やはりドミノ理論であった。

　　　身近な実例
　よい人生を送るためにはよい就職を、よい就職をするためにはよい大学へ、そのためにはよい高校へ、よい中学へ、よい小学校へ、よい幼稚園へ、……（そのためにはよい女房を、そのためにはよい就職を、……？）というのも、ドミノ理論と見られる。「よい幼稚園に入れなければ、よい人生が送れない」！？
　子供がよい幼稚園に入れれば、それにこしたことはない（もちろん「よい」ということの意味には問題があるが）。よい小学校やよい中学校に入ることも、それ自身は結構なことである。最近は子供を外国の中学校に送りだす親もいるが、それも立派な考え方であると思う。しかしそのために、あまり大きな犠牲を子供に強いることは、考えものであろう。
　このへんは判断の問題であるから、どこまでが「用心深い考え方」で、どこからが「詭弁」になるのか、はっきりした線をひくことはできない。しかし子供を外国に送りだすほどの勇気もない人が、小・中学生を毎日塾に通わせて、スポーツの喜びとか好きな本を読む楽しみを奪ってしまうのは、「怪しげなドミノ理論にひっかかっている」としか、私には思えない。
　アメリカでも、ジョンソン大統領は「バターも大砲も」と豪語していた。戦争を遂行しながら、生活水準を維持できると思っていたのである。それが戦争もままならず、国内のインフレや青年たちの心の荒廃など、思わぬ障碍にぶつかって、ついに退陣に追いこまれた。統一ベトナムが誕生した今、「将棋だおし」が起らないところを見ると、客観的には「一体何をやっていたんだ」ということになるが、世界の警察を任じていたアメリカとしては「われわれが努力したから、将棋だおしが防げたのだ」とか「感謝しているベトナム人もいるのだ」と考えているのかもしれない。
　これを教育界のドミノ理論にひきくらべてみると、なかなかおもしろい。「あれだけやったから、○○大学に入れたんだ」とか、「子供はけっこう楽しんでいる」など、主観的な判断を口にする人も多いが、これはアメリカの「いいわけ」と一脈あい通じるところがあるのではなかろうか？　何人かのベトナム人がアメリカの政策に感謝したからといって、「ぺトナム」が感謝したことにはならないし、逆境（？）の中にも楽しみがみつけられるからといって、「逆境が楽しい」というわけにはいかないのである。

詭弁術の総括

　　　健全な常識
　詭弁術にはいろいろな型があるから、手法や心得を簡単に要約することはむずかしい。しかし、基本的な対策としては、強弁術のときと同じように（あるいはそれ以上に）「健全な常識、健全な判断力を養う」ことが大切ではないかと思う。いかに力強い言葉で説得されようと、「だから、官憲も婦女子も、無差別に殺せ」 というのが結論であれば、断然はねつけるだけの理性は残さなければならない。
　「あなたの考え方には、ついていけません」 反論はこれで十分である。

　　　言葉の意味
　言葉の意味に注意するのも大切なことである。特に「本質的」とか「純粋の」などという形容詞か使われはじめると、言葉の本来の意味が消えうせて、ほしいままに使われるおそれがある。そのようなときは、なるべく具体的に「どういうことなのか」を説明してもらい、お互いの解釈に食いちがいが起らないように努力する必要がある。
　相手がごく普通の言葉を、特殊な意味で使っているときには、なおさら注意か必要である。
　ＡはＢ1（特殊な意味）である。
　Ｂ2（ふつうの意味）はＣである。
　ゆえに、ＡはＣである。
　これはすでに述べた媒概念曖昧の虚偽であるが、二番めの前提がごく当り前の主張であるときには、どうしても見のがされやすい。ひとつの例を挙げよう。
　Ａは水俣病患者（1）ではない。
　水俣病患者（2）でなければ、補償を受けられない。
　ゆえに、Ａは補償を受けられない。
　これは実際に論争をひきおこした例であるが、
　水俣病患者（1）＝水俣病の典型的な症状を、すべて具えた患者（医学用語）
　水俣病患者（2）＝工場廃水による、有機水銀中毒患者
という意味である。これらと、
　水俣病患者（3）＝審査会によって「水俣病」と認定された患者
という行政用語との差は、注目に値する。

　　　数字にダマされるな
　言葉の中で、特にダマされやすいのは数字である。数字の意味（どのように測定あるいは算出されたか）、単位の意味など、ある程度の専門知識がないと、わからないことが多いからである。これは昔からの大問題なので、『統計でウソをつく法』（Ｄ・ハフ著、講談社ブルー・バックス）という書物もあるくらいだから、先刻ご承知のことと思うが、全く触れないのも気か引けるので、簡単な例をひとつだけ挙げてみよう。
　「日本は水の豊かな国である」
実際、世界の年間降雨量をくらべてみると、およそ次のようになる（主要観測地点でのデータを平均したので、正確ではないが）。
　アメリカ　　　約800ミリ（ニューヨーク　1122ミリ）
　イギリス　　　約800ミリ（ロンドン　594ミリ）
　フランス　　　約750ミリ（パリ　585ミリ）
　ブラジル　　　約1700ミリ（サルバドール　1837ミリ）
　日　　本　　　約1780ミリ（東京　1503ミリ）
　このように、たしかに降雨量は多い。常識どおり水は豊かなように見える。―― ところが、これが案外アテにならないのである。
　水が豊かであるとは、ジャブジャブ使えること、つまりみんなが何百リットルも（あるいは何千トンも）使えるということであろう。それは、「ミリ」で測った降雨量では、わからないかもしれない。念のため、「受け皿」である土地の広さを掛けて、一年間に降る雨の総量を計算してみると、次のようになる。
　アメリカ 75200億トン
　イギリス　2000億トン
　フランス　4100億トン
　ブラジル　145000億トン
　日　　本　6600億トン
　これを人口で割って、一人当りの水の量を出してみると、
　アメリカ　35500トン
　イギリス　3500トン
　フランス　7900トン
　ブラジル　140000トン
　日　　本　6000トン
　これでは、日本はフランスより水が少ないではないか！
　どうやら正解は、「日本には雨がよく降る」ということで、特に「水が豊かである」とは 断定しにくいようである。

　　　数字をバカにするな
　だからといって、統計というものをバカにしてはいけない。水俣病でも、「工場の廃水があやしい」という疫学的な推定がついた時点で、とりあえず「浄化装置をつける」処置をとっておけば、被害をある程度軽減することができたはずである。わずかな見舞金で、それまで漁業組合を押えてきた会社の幹部には、余分の設備をつけることなど思いもかけぬことだったのだろうか？　それとも「発病の原因・機構がわからない」のでは、とるに足らないと考えたのであろうか？　しかし世の中には、「原因かわからない」ままに適切な処置をとり、多くの人々の命を救った人もいるのである。
　興味ある例は、ハンガリーの産婦人科医ゼンメルバイスの行動であろう。彼がウィーン大学で第一産科の助手になった頃（1844年）、産褥熱はヨーロッパ中の産科病院の悩みの種であった。出産はたいてい自宅で行なわれたが、合併症などで入院した女性は、原因不明の産褥熱のために高い死亡率（場所によっては25パーセントに達する）にさらされていたのである。当時は細菌学の知識がまだなかったから、病因は不十分な換気や「瘴気（しょうき）」（熱病を起させる毒気）とされていた。
　ゼンメルバイスが頭を悩ませたのは、彼の所属する第一産科での死亡率が、第二産科での死亡率の2～3倍にも及ぶということであった。それなのに、ふたつの産科の設備は全く同じで、違いといえば、第一産科では医学生を教え、第二産科では助産婦を教えることだけであった。そこで彼は、ほかの病室にも出入りする医学生たちが「何か」を運んでいるのだろうと考えて、本当の原因はわからなかったが、とにかく「手当の前に手を洗う」ことを学生たちに励行させた。学生たちが、わけもわからずに手を洗ったところ、その効果は劇的で、第一産科での死亡率は第二産科よりも低くなった。ハンガリーのペスト大学に移ってからの記録によれば、彼は産婦の死亡率を0.85パーセントにさげることができたという。

　　　正しい議論のための原則
　最後に、詭弁術に押されない、また気づかずに詭弁を操ったりしないための「心構え」を、要約しておこう。

　【原則１】無理やり説得しようとするな。
　無理を通そうとしたり、思いつきを口にしたりすると、かえって失言をして、議論がもつれることがある。また、いかに「当り前」と思えることでも、好き嫌いや人生観が関係するようなことについては、相手の趣味や判断を尊重しなければならない。もちろん、自分の考えにも（健全な常識に反するところがない限り）自信をもって、たやすく譲る必要はない。

　【原則２】時間を惜しむな、打ち切るのを惜しむな。
　議論は一歩一歩、お互いに一致できる点を確かめながら進めるとよい。そのように手堅く進めれば、論理のごまかしには、たいていダマされないですむと思う（相手がすばやくたたみかけてきたら、要注意である）。また意見の確認をするときには、言葉の解釈に食いちがいができないように、なるべく具体的な例にあてはめて、お互いの見解を確かめあうとよい。
　そうかといって、ムダに時間を費やすことはない。相手か強弁・詭弁を弄してきたら、もはや正しい議論は望めないので、惜しまず議論を打ち切ればよい。

　【原則３】結論の吟味を忘れるな。
　結論の現実性（実例にあてはめたときの、意義あるいは蓋然性など）、弱点などをはっきり認識しておくことは、いつの場合にも重要である。また健全な常識（道徳的、倫理的）に反する結論は、どんなに輝かしく見えようと、勇気をもって捨てなげればならない。天才はしばしば常識をくつがえす、というけれども、それは科学の世界のことであって、現実の社会でそうやたらと起ることではない（とはいえ、なかったわけでもないが）。

　【原則４】「わからない」ことを恥じるな。
　「わからない」ことを恥ずかしがる人は、論理の飛躍や二分法の押しつけに、簡単にダマされてしまう。いつでも「わかった」ところまで戻り、議論をやりなおしてもらう逞しさを身につけておけば、詭弁などにめったにやられるものではない。
　個々の戦術に対しては、次のチェック・ポイントを心得ておくとよい。

　【二分法に対して】
　（1）中間的な場合を考えなくてよいか。
　（2）開き直ったらどうなるか。

　【相殺法について】
　（1）相殺される事柄の、バランスはとれているか。
　（2）バランスがとれていないとしたら、どんな点での違いが重要か。

　【消去法について】
　（1）消去の仕方は乱暴でないか。見おとされている場合はないか。
　（2）結論は受け入れられるか。

　【ドミノ理論について】
　（1）「将棋だおし」が本当に起るのか。その現実性はどれくらいか。
　（2）ドミノ理論に従うための労力（プラス副作用）と、期待される結果（あるいは予防効果）とのバランスはとれているか。

　これだけの心得があれば、「鬼に金棒」で、あなたは議論を楽しむゆとりか持てるにちがいない。 ―― それでも実戦になると「あまりうまくいかない」という（私のような）人は、次の章の「論理のあそび」を楽しんでいただきたい。

やさしいパズル

 　やさしいパズルでは、答をみつけることよりも、その答を「誰にでもわかるように」説明できるかどうかが問題とされる。すぐに「そんなこと、当り前だ」という人でなく、鬼神をも哭かしむる、一万ドルの指輪を買った貴婦人をもほほえましむる説得力か必要とされる。まずはⅠ章の初級問題（13ページ）から始めてみよう。

　　　初級問題解答
　「十三人の客が十二の個室に、ひとりずつ泊れた」という説明を読んで、「あれっ」と思った人はいないだろうか？　もちろん「そんなはずはない」のだけれど、この説明だと……？
　「客の数のほうか多いのだから、みんながひとりずつ泊れるはずかない」
　これはいわば「結論」であって、説明の「どこ」がまちかっているかを指摘したことにはならない。
　問題は、１号室に入ったふたりの内容である。まず最後（十三番め）の客をかりに入れ、それからほかの客のひとりを到着順に入れたのだから、最初（一番め）の客が同室することになる。つまり１号室には「十三番めの客と、一番めの客」とが入ったので、２号室には二番めの客が、３号室には三番めの客が入るはずである。「三番めの客が２号室に」入ったとすれば、マネージャーはうっかり二番めの客のことを忘れてしまったのである！
　「でも、客室に入った順に、一番、二番と番号をつけたのなら、三番めの客が２号室になるでしょう？」
　しかしそれなら、十三番の人まで客室に入れなければ、全員が入ったことにならない。十二番めまで部屋に入れただけでは、残った一人（十二番めに到着した客）が忘れられたことになる。
　これはやさしい問題なので、誰でも落ちついて考えてみれば、すぐに「なあんだ」ということになるであろう。しかし一瞬ひっかかって「あれっ」と思った方もおられたかと思うし、あせったためにかえってわからなくなった方もおられるかもしれない。そういう人に対しては、下手に言葉で説明するよりは、絵でも描いてみせたほうがよい。「ひっかかる」場所は人によって違い、本人にはうまくいいあらわせないものである。いずれにしても、ひっかかった人は「頭の回転の早い人」（回転か遅ければ、決してひっかからない）、最初からゴマカシを見破った人は「冷静な人」と考えていただいてさしつかえない。

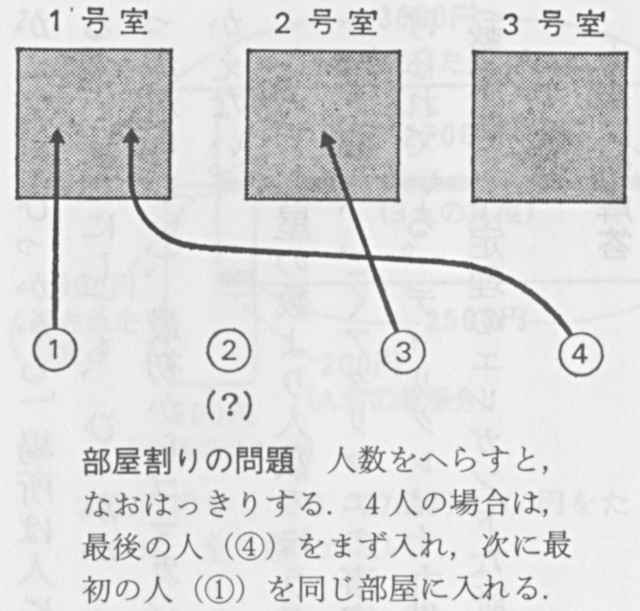
　なお、部屋の数より人数のほうか多ければ「どこかの部屋を二人以上にしなければならない」という、ごくアタリマエの事実には、ディリクレの部屋割り論法という立派な名前がつけられている。ディリクレは十九世紀の数学者の名前であるが、この事実を利用して、ある（整数論の）定理のエレガントな証明を与えた。

　　　中級問題解答
　Ｂ、Ｃ、Ｄは、一人九百円ずつ出したことになるので、三人の出費はあわせて二千七百円である。ここまでは正しい。その二千七百円がどのように使われたかというと、二百円をＡ君が着服し、二千五百円がレコードの代金として支払われた。いいかえれば、三人の出費二千七百円からＡ君の着服した分二百円をひくと、本当のレコードの代金二千五百円になる。もともと、Ａ君が着服した二百円は、三人の出費二千七百円の一部分なので、「二千七百円にＡ君の着服した二百円を加える」のではＡ君の着服した分を二重にかぞえただけであり、出てくる「二千九百」という数字には何の意味もない。
　最初の三千円は、どこに行ったのだろうか？　二千七百円か出費となり、三百円は戻ってきた。つまり、三人の出費二千七百円に、戻ってきた三百円を加えれば（戻す前の）最初の三千円に一致する。このように「戻ってきた三百円」を加えるべきところを、似て非なる数字「Ａ君が着服した二百円」を加えているので、その差かちょうど「不足の百円」になっているわけである。

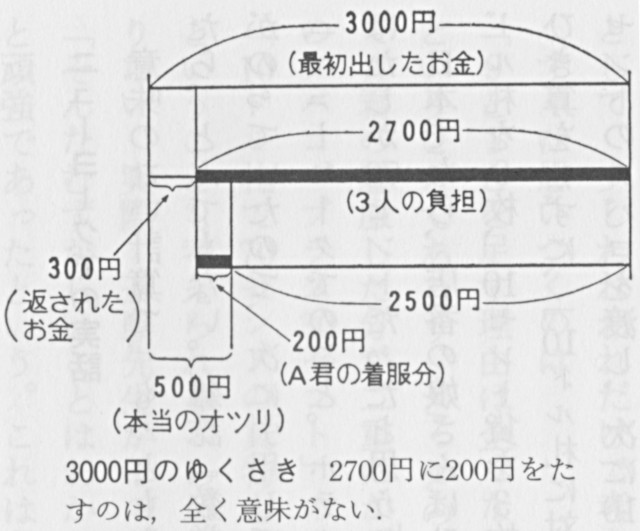
　この問題のうまい（ずるい）ところは、金額の差が小さいところである。差が大きすぎると「計算の仕方がおかしいんじゃないか」と疑われやすいが、百円ぐらいだとつい計算を信用して、「どうして百円足りないんだろう」と首をひねる人も出てくるわけである。そういう人は、「不足の百円」などという表現にダマされたすなおな人であるから、「本当に百円足りないのか？」「そもそも、二千九百という数字に、どんな意味があるのか？」という順に話を進めれば、すぐにわかってもらえると思う（上図のような絵が、役に立つにちがいない）。

＜以下略＞

詭弁論理学改版 （中公新書） [ 野崎昭弘 ] 価格：792円（税込、送料無料) (2020/1/2時点) 楽天で購入