論理的思考の技法（１）

目次

　第２版まえがき
　まえがき

　第1章　論証の構造をつかむ
第１節　論証とは　2　　／　　問題１　6
第２節　前提と結論の関係　11　　／　　問題2　14
第３節　矛　　盾　19　　／　　問題3　22 論証図の練習問題にチャレンジ！　28

　第２章　条件法
第１節「ならば」という言葉　32
第２節　逆・裏・対偶　35　　／　　逆・裏・対偶の練習問題にチャレンジ！　　38　　／　　問題4　39　　／　　問題5　47　　／　　COFFEE BREAK 二重否定　51　　／　　COFFEE BREAK 赤い部分は駐停車禁止　52
第３節　隠れた条件法　54　　／　　問題6　55　　／　　問題7　59　　／　　COFFEE BREAK 風が吹けば桶屋がもうかる　―― 推移性　63
第４節　「だけ」・「のみ」と必要条件・十分条件 67　　／　　問題8　67　　／　　COFFEE BREAK 回答者のみ購入可　76　　／　　問題9　82　　／　　COFFEE BREAK 記号化　85
第５節　真理表　88　　／　　問題10　88
第６節「ならば」の問題上級編　96　　／　　上級問題1　96　　／　　上級問題2　104　　／　　COFFEE BREAK ド・モルガンの法則　107
第７節　条件法のまとめ　108 復習問題1　108　　／　　復習問題2　111　　／　　まとめの問題　115　　／　　練習問題にチャレンジ！　118

　第３章　否定
第1節　反論　123　　／　　COFFEE BREAK　質問と反論を考えよう　131
第2節　否定　135　　／　　COFFEE BREAK　「必要」ってどんな意味？　138　　／　　問題12　148　　／　　COFFEE BREAK　「進化」152
第3節　矛盾律と排中律　153

　練習問題 ―― 解答編　159
　あとがき　185
　事項索引　187 　

まえがき

　本書は，『受験新報』に2002年6月から筆者が連載した「論理的思考の技法」という小文を，「ならば」という言葉を中心にまとめなおしたものである。全体の構想をきちんともって始めた連載ではなかったこともあって，ばらばらに述べた事柄もあったが，本書ではそれを話題別にまとめなおして加筆し，練習問題も多くつけたので利用はしやすいのではないかと考えている。第3章の「否定」の部分はほとんど書き下ろしである。
　練習問題は，アメリカのロー・スクールの入学試験であるＬＳＡＴを参考に例題を作ったものもあるし，論理学の教科書に出てくる問題をふくらませたものもある。法科大学院の適性試験に見られるタイプの問題も複数とりあげ，受験を考えている人に役立つよう配慮した部分もあるが，なんであれ書かれたものを読みそれを理解したり論じたり，議論をしたり人を説得したりするさまざまな場面で，「論理的に考える」ためには何に気をつければよいのか，という点を伝えることを主眼にした。レポートを書いたり，論証を要約したり検討したりするときにも役立つよう心がけたつもりである。
　ところで，読者のみなさんはマイン・スウィーパーというゲームをご存知だろうか。 ＷＩＮＤＯＷＳに標準装備されているゲームだが，非常に単純で頭を空っぽにできるので，私は気分転換にこれでときどき遊ぶことがある。そしていつもこれは論理ゲーム以外の何ものでもないなと感じる。
　「マイン」とは地雷であるが，地雷のある場所を推理して，地雷のあるマスにはマークをつけ，それ以外のマス目をすべてあけていく速度を競うゲームである。手がかりは，あけたマス目に書いてある数字である。「1」と書かれたマス目に接して地雷が1個ある。「5」とあれば，それに接して5個の地雷があるわけである。「1」のマス目に接して1個の地雷が見つかれば，「1」の周りのそれ以外の7個のマス目にはもう地雷はないので安心してマス目をあけ，どんどんヒントをふやしていく。「1－2－1」と数字が並んでいて，たとえばその3つのマス目の上に地雷がなければ，［2］をはさんで地雷が1個ずつあるのだなと推理する。つまり，この数字の並び方なら，地雷の並びはこの可能性とあの可能性しかないと「ならば」で推理を進め，手詰まりになったら別の「こうならこう」という「ならば」を使って推理を進めていく。数字の並び方のパタンをたくさん身につけていればそれだけ推理は簡単で正確になる。
　本書で筆者はこの数字が書いてあるマス目を示し，どういう並び方のときにはこういう形になっているので気をつけてということを述べようとした。勢いあまって自ら地雷を踏んづけてしまったこともあったが，読者のみなさんが落とし穴に落ちず，森のなかで迷ってしまわずに目的の場所ヘスマートに到着するヒントにしていただければ幸いである。
　　　2004年10月　　　鈴木美佐子

論証とは

　みなさんが何かを「論理的である」と称するのはどんなときだろうか。そしてそれは何に対してだろうか。すぐに思いつくのは，「論理的な人」，「論理的な文章」，「論理的なものの考え方」といった表現だろう。

　〇論理的なのは？
　Ｋ，Ｓ，Ｍの３人がレストランに入った。ウェートレスの「何になさいますか」との問いに，

　Ｋ「カレーライス」
　Ｓ「今日は暑いからドリア」
　Ｍ「Ｋさんと同じもの」 と３人は答えた。

　さて誰が一番論理的か，あるいは論理的でないか。ＳかＭが論理的でないと答えた人はなぜそう考えたのか。心理テストじゃあるまいし何を食べるかで論理的かどうかなんてわからない，と考えた人は正しい。これだけの材料から誰が論理的かを判断せよというのは無理である。
　では３人に注文の理由を聞いてみよう。

　Ｋ「私は知らないレストランではカレーを注文することにしている。カレーが一番当たり外れがないから」
　Ｓ「さっき言ったよ。暑い日だからだ」
　Ｍ「Ｋさんが好きだから」

　これなら判定できる，と思った人はなぜそう思ったのか。かりにあなたがＫを論理的だと考えたとしよう。Ｋが最初に言ったのは「私はカレーライスを注文する」ということだ。あなたは「カレーライスを注文する」だけではＫを論理的であるなどと思わなかった。
　理由を聞かれてＫは「ここは初めて入ったレストランだ。初めてのレストランでは何がおいしいかわからない。何がおいしいかわからないなら当たり外れのないものを注文したほうがいい。当たり外れがないのはカレーだ」と言ったわけである。あなたはＫの言うことをもっともだと感じ，なるほどＫの示した理由なら「カレーを選ぶ」ということが出てくるな，と思う。そしてＫを論理的だと考えた。
　つまり，あなたが「論理的」と言ったのは，「カレーライスを選んだ」ことでも，「当たり外れがないのはカレー」と考えていることでもない。「カレーを選ぶ」理由が「カレーに当たり外れがない」ことだと述べた点，「理由から最初の主張が出てくる」という点なのである。すなわち私たちが「論理的」と判断するのは，発言の内容ではなく，言ったことと理由との関係に対してなのである。もっとくわしく言うなら，主張を述べた文と理由を述べた文が「もっともな」，「出てくる」関係にあることを「論理的」と言っているのである。

　〇論理的でないのは？
　論理性が現れるのは，述べられたこと（主張）とそれを述べた理由（根拠）の間である。ではその間の関係がどうであれば「論理的」なのか。1つのキーワードは「出てくる」であるが，典型的に「論理的」な事柄を示しても，あまりにありふれていてピンとこないため，ここでは逆に「論理的でない」ものを見ることで裏側からこの言葉の対象となる「関係」にも う少し光を当ててみよう。
　ＳとＭについてはどうだろうか。2人の理由に対し即座になるほどとうなずく人はそれほど多くないだろう。Ｓは「暑いからドリアを注文する」と言った。Ｍは「自分はＫさんが好きなので，Ｋさんと同じものを選ぶのだ」と言った。私たちがそれを「もっともだ」と思わないのはなぜなのか。
　Ｓについて言えば，「今日は暑い」ということから「ドリアを食べる」ということがどうして出てくるのかわからないからだ。すなわち，「暑い」が「ドリアを食べる」の理由になっているとは思えないからだ。両者は理由と理由づけられるものの関係にあるとは認められない。
　そんなとき私たちはさらに「なんで暑いとドリアなのさ」と聞く。Ｓは「長寿村の人に聞くと暑い時は熱いものを食べる習慣があったと新聞に書いてあった。一番熱そうなのがドリアだったから」と答える。私たちは「ふーん，なるほどねえ」くらいのことを言うかもしれない。しかし「でもね…」と続けたくなりはしないだろうか。
　あなたがＳの言ったことを実にもっともだと感じ，彼の説明を論理的だと思うのでなければ，このあとを続けてみてほしい。正解は一通りというわけではない。
　1つの続け方はこうだ。「新聞に書いてあったからって，暑いときに熱いものがいいというのがどうして出てくるのさ。まず，新聞に書いてあることが正しいとはかぎらないし，かりにそういう習慣の人が長生きだったとしても，君がそうしたからって長生きするとはかぎらないだろう。もっ と論理的に考えるべきだよ」。
　Ｓの発言と理由を若干くわしく補足しつつまとめてみるとこうなる。
①長寿の人は暑いときに熱いものを食べる習慣があったと新聞に書いてあった。
②新聞に書いてあることは正しい。 したがって
③長寿の人には暑い時に熱いものを食べる習慣があった。 ゆえに
④暑いときに熱いものを食べれば長生きする。 そして
⑤私は長生きしたい。
⑥今日は暑い。 だから
⑦私は熱いものを食べる。また
⑧ドリアは熱い。 ゆえに
⑨私はドリアを選ぶ。

　 〇論証：結論＋前提
　少し複雑だが，Ｓの「ドリアの選択」と「その理由」の関係はこうである。①「新聞記事」と，②「新聞記事は正しい」という理由から，③「長寿の人は暑いとき熱いものを食べる」と言える。さらに，③だから④「暑いとき熱いものを食べれば長生きする」と考える。④と⑤「長生きしたい」，⑥「今日は暑い」という理由で⑦「熱いものを食べる」が出てくる。⑦に加えて⑧「熱いのはドリアだ」ということから⑨「ドリア」ということになるわけである。図示すると次のようになる。

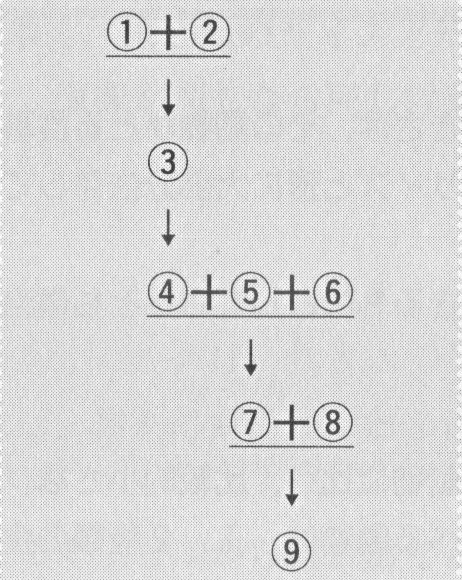
　私たちがＳの説明に違和感をもつのは，１つには「③だから④だと考える」からである。④と考える理由を③だとＳは言うわけだが，③は④の理由になっていない。長寿の人にそうした習慣があったとしても，習慣がある人がみな長生きするとはおよそ言えないからである。両者の関係は「理由になる」関係ではない。だから私たちはＳを論理的でないと感じるのである。つまり，「論理的でない」のは「一方から他方が出てくる関係ではない」ということであり，Ｓが両者の関係を誤って捉えているから「論理的でない」と言っているのである。
　このように「理由から何かの主張を導出する（図の↓）」ことを「推論する」と言い，「○○から□□が出てくる／言える」ことを「推論」と言う。 ○○には理由（根拠・前提）が，□□には主張（結論）が入る。また，結論の理由を示して結論が正しいことを示すことを「論証する」と言うが，その区別はともかく，推論や論証は根拠と結論が必ずセットになっている。「論理的」という言葉はもっぱらこの推論や論証について言われるということを意識してほしい。

「ならば」という言葉

　論理学にかぎらず，論理が問題になる場面でまちがいやすいのが「～ならば…」に関してである。意識せず使っていることも多く，そのためにさまざまな形の誤りが生じている。本章でしっかりと全体像をつかまえよう。

　〇接着剤の働きをもつ言葉

　言葉は多くの場合，ものや出来事，状態などを指して使われる。「大きな音がした。そして花火が上がった。菊，あるいはバラのイメージだ。あの雲がなかったならばもっときれいだっただろう」という文章で，「花火」や「菊」はものを，「上がる」は動きを，「きれい」は状態の評価（あるいは見た人の心の状態）を，「花火が上がった」という文は出来事を指し示している。これに対して，「そして」・「あるいは」・「なかった（ない）」・「ならば」といった言葉は，何を指しているのだろうか。これらの言葉は何も指していない。それは，語や文を結びつけ関係づける「接着剤」，あるいは「連結器」の役割を果たしている。
　言葉や文を結びつけるものは他にもあるが，「ない」・「そして（かつ）」・「あるいは（または）」・［ならば］という4つの言葉が，なかでももっとも基本的なものである。接着剤にも仮どめをするような糊，一度くっつけたらはがせない強力な接着剤，化学変化を起こさせてしまう糊などいろいろな種類があるように，この4つの言葉も連結の仕方が異なる。そのなかでも「ならば」は，私たちの思考にとって大変強い力を発揮する言葉である。
　私たちがいろいろな事柄を調べ，探求し，考え，検証し，その結果手に入れるものは，ある意味で「こうであるならばこうなる」という判断だということができる。低気圧が通過すれば雨が降り，故意に人を傷つければ傷害罪となり，ある成分を含んだ薬剤が投与されれば痛みが緩和される。私たちはこうした判断をもっていることで，天候を予測したり，治療をしたりすることができるのである。少々乱暴に言ってしまえば，正しく「推論する」ということは「ならば」でつなげられた真の命題を獲得することである。
　また，α1からαnまでの情報が与えられ，そこからβという結論を導出する（推論する）とは，「α1＆α2＆…＆αｎならばβ」という判断を得て，「α1，…，αｎ」なのだから，βだと判断するということである。
　このような大きな力をもった「ならば」は，一方でなかなか厄介な言葉でもある。味方につけると心強いが，勘ちがいを引き起こしたり落とし穴につき落としたりする言葉でもある。「ならば」をよく理解し，苦手意識をなくすことが論理的思考を身につけるための第一関門である。「ならば」をめぐる問題をじっくりと考えてみよう。

　〇「ならば」のいくつかの意味
　「～ならば…」という言葉は，日常生活ではいくつかの異なる意味で使われている。
（1）風が吹けば桶屋がもうかる。
（2）将を射んと欲すればまず馬を射よ。
（3）許可なく使用すれば罰金をいただきます。
（4）金を出せ。さもないと（そうしなければ）殺すぞ。
　 （1）は，「風が吹く」という出来事が原因となり「桶屋がもうかる」という事態を引き起こすということを意味し，原因と結果の関係を「ならば」は示している。（2）の「ならば」は，「将軍を射落とす」という目的を達成するには，手段として「将軍の乗っている馬を射る」という手段が必要だということを意味する。（3）は，「無断使用」という行為が「罰金」という処罰にあたるという規則を述べている。（4）は，「金を出さない」ことが「殺害」の原因になるが，「金を出す」ことによってそれが避けられるという意味である。
　こうしたいくつかの意味のちがいを明確にすることはここではおこなわない。「ならば」を，2つの文をある形で結びつけるものとしてのみ考え，その最小の役割を考えていくつもりである。簡単に言えば，「事実としてそれが起こっていようといまいと，そうだと仮に考えてみると，こうなる」というような意味で，2つの文を結びつけているものが「ならば」だと理解しておいてほしい。英語の「if…，then～」と同じ意味だと考えてくれればよい。

逆・裏・対偶

　 〇4枚カード問題
　テーブルに4枚のカードが置かれています。片面には文字，片面には数字が書かれています。みなさんから見えるのは，「知」，「キ」，「8」，「17」です。「漢字の裏は偶数だ」という仮説が正しいかどうか確かめるには，最低どのカードをめくる必要があるでしょうか。
　筆者はこの問題を，「ならば」をめぐる問題を考える授業の初回に出してみることにしている。「『知』と『8』だと思う人は手をあげてください」というと，半数以上の人が手をあげる。しかし，これは正解ではない。4枚のカードのうち，「キ」の裏がどうでもいいことは誰にでもわかる。「漢字の裏」が問題なのだから「知」はめくってみよう。次に何をめくるか。多くの人は偶数という言葉が出てくるために，「8」もめくらなければならないと思ってしまうようだ。
　「8」のカードをめくる必要はない。なぜなら私たちは「偶数の裏は漢字である」という仮説を確かめているわけではないからである。たとえば，偶数の裏がひらがなだったとする。そのとき確かめたのは「偶数の裏はひ らがなだ」ということであり，ひらがなの裏に偶数が書かれていようと奇数が書かれていようと，「漢字の裏は偶数だ」という仮説には無関係である。
　「知」はもちろんめくらなければならない。これをめくらないと「漢字の裏は偶数」かどうかがわからない。そして重要なのが「17」をめくってみることである。というのも，この仮説を確かめるためには，「17」の裏に漢字が書かれていないことを確かめる必要があるからである。もし「17」の裏に漢字が書かれていれば，「漢字の裏は奇数」ということになって，「漢字の裏は偶数」がまちがいになる（反証される）。仮説が正しいということを確かめる（確証する）には，奇数の裏が漢字でないことを確かめる必要があるのである。
　この問題のなかに「ならば」という言葉は出てこないが，実は「条件法の文」がポイントの問題なのである。

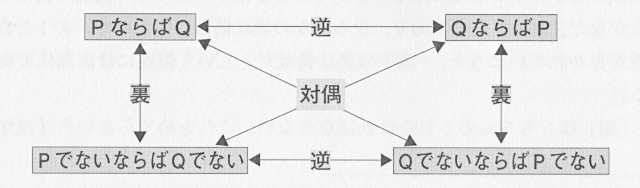
　〇逆・裏・対偶
　「もしＰならば，Ｑである」という形の文を，以下では「条件法の文」と呼ぶ。これは，一定の条件Ｐがみたされていると仮定すると，あることＱが成立することを主張する文である。
　前述の「風が吹けば桶屋がもうかる」もそうであるし，広告で目にする「レシート集めて100万円ゲット！」という文も条件法の文である。この文は，「合計いくらのレシートを集めるならば，抽選で100万円が当たります」ということを述べている。
　条件法の文「ＰならばＱ」について，以下の約束がある。
　①　条件を述べるＰを「前件」と呼ぶ。
　②　条件が成立したときに成立すると主張されているＱを「後件」と呼ぶ。
　③　条件法の文をもとにして「逆」・「裏」・「対偶」と呼ばれる文を作ることができる。
　前述の「4枚カード問題」を例にとれば，逆と裏と対偶は次のようになる。

仮説：カードＸの片面が漢字ならば，カードＸの片面は偶数だ。
逆　：カードの一方の面が偶数ならば，カードの他方の面は漢字だ。
裏　：カードの一方の面が漢字でないならば，カードの他方の面は偶数ではない（奇数だ）。
対偶：カードの一方の面が偶数でない（奇数である）ならば，カードの他方の面は漢字ではない。

　条件法の文が正しいとき，対偶も正しくなる。
　くわしくはあとで見るが，たとえば「水なら無臭だ」が正しいときには，「無臭でないなら水でない」と言える。しかし，逆と裏はそうではない。「無臭なら水だ」（逆）とはかぎらないし，「水でないなら無臭でない」（裏）ともかぎらない。
　4枚カード問題は，仮説であるもとの条件法の文「漢字ならば偶数」を「知」をめくることで確かめ，「偶数でない（奇数である）ならば漢字でない」という対偶の文を「17」をめくることで確かめているのである。カードの片面が偶数（「8」）のとき（逆）や，漢字でない（「キ」）とき（裏）はどうであろうと関係はない。

「だけ」・「のみ」と必要条件・十分条件

　[問題8]
　｢中身と分離したときに不要にならないものは，容器包装ではない｣と同じ意味になるものを次の(1)～(5)のなかから１つ選びなさい。
　　(1)中身と分離したときに不要になるものは，容器包装である。
　　(2)中身と分離したときに不要になるものは，容器包装だけである。
　　(3)中身と分離したときに不要になるもののみが，容器包装である。
　　(4)容器包装でないものは，中身と分離したときに不要とはならない。
　　(5)容器包装だけが，中身と分離したときに不要になる。

　これは筆者の知るかぎりでは，野矢茂樹氏が『論理トレーニング101題』の「逆は必ずしも真ならず」の項で示した例題である。「容器包装リサイクル法」が施行されたときの通産省（現在は経済産業省）の説明が上記問題文の「中身と分離したときに不要にならないものは，容器包装ではない」というものだったのだが，どうも理解しにくい。この説明に対し，「中身と分離したときに不要になるものは容器包装だ」と言えばわかりやすいという投書があった。それを取り上げ，条件法の練習問題としたものである。投書者の提案はもとの文の裏となっており，もちろん正しい言い換えではない。
　もとの言い方では1つの文の中に否定が二度も使われており，わかりづらいことは確かである。しかし「裏」の形に言い換えたのでは，不要物全部が容器包装ということになってしまう。たとえば，洋服を買うとタグなどについている値札やブランドやサイズを書いてある札は中身（洋服）と別にできて，中身を使うのに不要だが，容器包装ではない。不要になるものにも容器包装でないものがあるので，「裏」の形の文「不要なら容器包装」では同じ情報を伝えたことにならない。
　ではどう言い換えればよいのか。もとの文を省略して条件法の形で書くと，

[1]不要でないならば容器包装でない。

　となる。選択肢(1)は投書者の提案と同じ「不要ならば容器包装だ」で，もとの文の「裏」である。（4）は「容器包装でないならば不要ではない」であり，もとの文の「逆」となり，［１］の正しい言い換えではない（（1）と「対偶」になり，（1）と同じことを伝えている）。
　それ以外の選択肢には，「だけ」や「のみ」という言葉が含まれているので注意を要する。
　(2)不要なものは容器包装だけだ。
　(3)不要なもののみが容器包装だ。
　(5)容器包装だけが不要になる。
　(2)は，不要なら容器包装で，不要なものはそれだけ，と言っている。すなわち，「容器包装でないものは不要でない」ということである。また，(5)「容器包装だけが不要」も「不要なものは容器包装以外ない」ということなので，「容器包装でないなら不要でない」と述べている。つまりこの2つの文は，（1）・(4）と同じ「不要ならば容器包装だ」ということを述べている。
　（3）はどうだろうか。「不要なもののみが容器包装だ」は，「不要でなければ容器包装ではない」，すなわちもとの文[1]と同じであり，[1]よりわかりやすい言い方になっている。
　「のみ」，「だけ」のような言葉が現れ条件法の文と同じ意味をもつ文については，前節で書き換えのコツを説明したが，もう一度整理して，「だけ」・「のみ」の構造をしっかりおさえておこう。
　「のみ」や「だけ」といった限定表現がおこなっているのは，限定表現がくっついている部分の述べていることが成立しないと，もう片方も成立しないということである。「ＡのみＢ」という文は「Ａ」に「のみ」という限定表現がつけ加えられているが，これが述べているのは「Ａが成立しないとＢが成立しない」ということである。なぜなら，ＡのときにのみＢなのだから，ＡでなければＢでないことになるからである。述語のほうに「のみ」がくっついていても考え方は同じである。「ＡはＢのみ」は「ＡであるのはＢであるときのみ」なのだから，「Ｂが成立しないとＡは成立しない」のであり，［ＢでなければＡでないのである］。つまり，限定表現が付加されている文は，限定表現がくっついている部分の否定が前件になり，残りの部分の否定が後件となる条件法と同じ意味をもつわけである。

　 ★Ａであるときにのみ（だけ）Ｂ
　⇔ＡでないならＢでない
　⇔ＢならばＡ

　 ☆ＡであるのはＢだけ（のみ）だ
　⇔ＢでないならＡでない
　⇔ＡならばＢ

　 〇「だけ］・「のみ」再び
　上記のような説明に対して読者から，「不要なもののみが容器包装だ」は，①「不要なものが容器包装だ」と②「不要でなければ容器包装でない」の2つの意味をもっているはずなのに，①を考慮に入れてないのではないかとの質問が寄せられた。質問はもちろん，その説明も興味深いものだったので，これを取り上げ，さらに「必要条件・十分条件」という観点からもう一度考えてみよう。

　〇申込者は必ず入場できるのか
　質問者のあげている例は，
　<1>事前申込者のみが入場できる。
という文である。筆者の解説によれば，この文は，
　<2>事前申込みをしていない者は入場できない。
という意味になる。そのとき<2>は「申込者が入場できるかどうか」については述べていないが，<1>は「申込者は入場できる」ということを述べている。したがって，<1>は<2>と同じ意味ではないと質問者は指摘する。その説明として，<1>を見て申込みをした男性が会場にやってきて入場しようとすると，「<1>は『申込みをしていない人は入場できない』という意味です。実はさらに条件があって女性じゃないとだめなんですよ。あなたは入場できません］と言われたら，その人は詐欺だと怒るだろうと述べている。
　確かに怒るだろう。そして質問者は，この男性が怒るのは，「事前申込者のみが入場できる」が「事前申込者は入場できる」という意味をもつからだと考えている。
　なるほどと思った人も多いのではないだろうか。この人が怒っていることを理不尽には感じないし，怒ることがもっともなら，「申込者は入場できる」という意味のはずだと考えてしまうかもしれない。しかし，この男性が怒っているのは実は別の事柄についてである。イベントの告知に「申込者のみが入場できる」とあり，他に何も書かれていなければ，通常は「申し込めば入場できる」と思ってしまう。
　そう思ってしまうのは，「事前申込者のみ入場できる」が「申し込めば入場できる」という意味を含むからではなく，他に条件が何も示されていないからである。これは条件の示し方が適切か不適切かという問題であって，条件法の文の意味の問題ではない。事前申込みが必要であること以外に，女性であること，18歳以上であることなどといった条件が他にもあるのであれば，それを一緒に明示しないのは不適切である。そういった不適切さ，不親切さに対して入場を断られた男性は腹を立てたのである。

　〇「ＡのみＢ」の意味
　「申込者のみが入場できる」から「申込者は入場できる」という文を常に導くことはできない。それは，その文が<2>の裏にあたることからも明らかである。しかし，この質問は考えておくべき重要な問題を提起している。それは「申込者のみ入場可」の文の条件を述べた部分が必要でなおかつ十分な条件ではないという点である。すなわち，この文で「申込みをする」という条件は「入場」に必要ではあるが，入場をするための十分な条件ではないということである。
 「ＡのみＢ」という文は，実はＡについての文というよりも，Ｂであるための必要条件を示す文である。入場できるための必要条件が「事前申込み」なのである。したがって，「申し込んで入場できる」こともあれば，「申し込んだが入場できない」ということもありうるわけである。このどちらとなるかは，状況やＡとＢの内容によって決まるのであり，「ＡのみＢ」という文の構造から決まるのではない。内容と無関係に「ＡのみＢ」という文から導けるのは，先に説明したように「ＡでないならＢでない」である。

　〇必要条件と十分条件
　別の例で考えてみよう。

　[1]　履修登録者だけが単位を取得できる。

という文がある。この文は「登録をしていない人は単位取得できない」ということ，［履修登録が単位取得の必要条件である］ということしか述べていない。すなわち，

　[2]　履修登録しないなら単位取得できない。

ということである。登録したら取得できるのか，他にクリアしなければならない条件があるのかについては何も述べられていない。そして，履修登録をしたからといって単位をとれるとは必ずしも言えないのはもちろんのことである。出席が足りなかったり，試験で合格点に達さなかったりすれば，単位はもらえない。このようなとき，履修登録は単位取得の十分条件ではないと言われる。十分条件であるためには，[2]の裏，

　[3]　履修登録すれば単位を取得できる。

という文が成立していなければならない。この場合には，履修登録さえしていれば単位取得できるのだから，履修登録は単位取得の十分条件である。
　一般化するとこうなる。
「ＰならばＱ］が成り立つとき，
ＱはＰの必要条件であり，
ＰはＱの十分条件である。
　 それに加えて、「ＱならばＰ」も成り立てば、 ＰはＱの必要十分条件である。
　ＰがＱの十分条件ということについては理解が容易だろう。「ＰならばＱ」が成り立っているとき，Ｐが成り立っていれば必ずＱが成り立つのだから，Ｐさえ起こっていればそれだけで十分Ｑは起こる。しかし，「ＰならばＱ」のＱがなぜＰの十分条件（本書ではこう書いてありますが「必要条件」が正しいのではないだろうか？）なのかはわかりにくい。必要条件を理解するためには前述の限定表現を思い出すとよい。
　「ＰのみＱ」は「ＰでないならばＱでない」であり，ＰはＱであるための必要条件であった。Ｑであるためには最低限必要な条件としてＰがクリアされていなければならないということである。これを対偶の形にすれば「ＱならばＰ」ということである。つまり，後件Ｐは前件Ｑの必要条件なのである。したがって，履修登録は単位取得の必要条件ということになるのである。

　〇何が必要で，何が十分か
　必要条件，十分条件，必要十分条件をこのように定義することは簡単であるが，実際に何が必要で，何が十分で，何か必要十分なのかを理解するのはなかなかむずかしい。
　先日こんなことがあった。筆者が出勤しパソコンの電源を入れメールを受信しようとしたが動かない。別のパソコンでメールチェックしたら受信できた。メーラーが壊れているにちがいないと判断し，くわしい人に見てもらったところ，メールソフトには何の問題もなく，当のパソコンのＬＡＮケーブルが外れていたことが原因だった。
　筆者は「メーラーが正常で，受信をクリックすれば，メールが受信できる」と考えていたのである。ところが，「受信タブをクリックしても受信できない」。したがって，「メーラーが正常でない」と結論した。この推論自体に誤りはない。では何がおかしいのか。それは，前提としている条件法の文の前件が後件の十分条件ではなかったのである。つまり，筆者が採用した前提はまちがいであったということである。
　同僚がメーラーを点検しても異常はない。つまり「メーラーが正常でない」は誤りであった。そして「メール受信できない」のだから，「メーラーは正常で，クリックしてもメールを受信できない」ということになる。これは前件が正しいのに後件が誤りという「ならば」の文が誤りになるケースに該当する。すなわち，条件法の文（前提）がまちがいということである。筆者が十分条件と考えていたものは必要条件に過ぎなかった。つまり，言えるのは「メーラーが正常でないなら，受信できない（受信できるなら正常）」ということに過ぎず，ケーブルがつながっている，サーバーがダウンしていない，といったそれ以外の受信のための必要条件を見落としていたのである。
　少々大げさな言い方かもしれないが，私たちは，いろいろな出来事や現象を経験して，「こうなったならばこうなる」という仮説を立てる。それに反する出来事が起こったとき，仮説に固執していたのでは新しい発見はない。条件がほんとうに成立していたのかを検証し，そうであったのなら，条件はそれだけではなく，他にもあったのではないかと考えることが必要である。条件をほんとうに十分な条件とするために，観察を重ね，検証して，仮説を修正・改善していくのが，私たちの思考活動である。
　こんなこともある。成績が発表されて学生が問い合わせにきて，「授業に毎回出席してレポートも出したのになぜ不可なんですか」と言う。確かに学期の初めに「合格するためには授業に出席してレポートを提出しなければなりません」とは言った。これは「出席してレポートを出さないと合格しない」ということであって，「出席し，レポートを出すならば，合格する」とはちがう。前述の「のみ」に関する説明でも述べたが，「出席とレポート提出」が合格の必要十分条件とみなされることが多いのは，「ならば」や「ために」が現れる文の形式によるのではなく，「出席」，「レポート提出」，「合格」の内容から，これで十分と受け取る側が考えてしまったということである。筆者はこの学生に「必要条件と十分条件を取りちがえるようでは論理学の授業が不可でも仕方がない」と言えばよかったと思っている。

　〇十分だが必要ではない
　逆に十分条件を必要条件と取りちがえる誤りもある。十分なものがあれば必要なものは含まれているはずだから，十分条件は必要条件だと考えてしまう誤りである。
　Ｑの十分条件をＰ，必要条件をＲとしよう。そうすると。
　1）ＰならばＱ
　2）ＱならばＲ
の両方が成立していることになる。「ＰならばＱ」で，「ＱならばＲ」なのだから，「ＰならばＲ」となり，ＰはＲを必要条件として含む。この意味で，十分条件は必要条件を含むと言ってもよい。しかし，ＰがＱの必要条件であるためには，「ＱならばＰ」が言えなければならない。これは，1）からも2）からも出てこない。具体例で考えてみよう。
　単位取得の十分条件は，たとえば成績表に「優」と記載されていることであり，必要条件は試験に合格することであるとしよう。そうすると，
　3）成績が優なら単位取得しでいる。
　4）単位取得しているなら試験合格である。 と言える。それゆえ，
　5）成績が優なら試験合格である。
　成績表に優がついていれば確かに試験は合格していると言える．この意味で優は合格を含む．しかし，単位取得のために優である必要はない。この教員がたとえば試験で81点以上をとった人に優をつけていて，合格ラインを60点としてそれ以上の人に単位を与え，70点までを可，80点までを良にすることにしているとすると，単位取得のために優をとる必要はない。優は単位取得の必要条件ではない。
 必要条件・十分条件と「のみ」の関係をまとめておこう。

　ＡのみＢ
　ＡでないならばＢでない（ＢならばＡ）。
　 ＡはＢの必要条件であり，必要十分条件ではないので，
　Ａを満たしているからといって，
　 Ｂであるとはかぎらない。

反論

　論証に反論するということについては，第1章後半の「矛盾」に関する箇所でふれ，着眼点についてまとめておいたので参照してほしい（24頁）。いくつかポイントはあるが，重要なのは，事実関係に目を奪われるのではなく，第1に論証の構造をきちんと把握すること，第2に前提と主張との関係に注目することである。例をあげて説明していくが，まずここで1つ 確認しておきたいのは，「反論」とは「相手の主張と違う意見を述べる」ことではないという点である。 　会議などで経験したことがあるかもしれないが，たとえば「イベントを成功させるためには宣伝が大事だからパンフレットを作るべきだ」と主張している人に，「成功させる方法は宣伝だけとはかぎらない。興味のない人たちがたくさん集まったところで成功とは言えないのではないか」と批判的意見を述べたりすると，「では，君はこのイベントが成功しなくてもよいというのか」といった反応が返ってくることがある。反論することと，相手の主張に反対し，別の対立意見を述べることは別のことである。 　このやりとりでは，「イベントを成功させたい」という点では意見は一致しており，その前提を共有している。しかし，「成功させたいなら，人がたくさん来てくれることが必要」とはかぎらない。反論者は「このイベントの成功とはどういうことか」という疑問をもち，その点を確認しようとして「成功＝集客」という前提に疑義を提出しているのである。この意見にきちんと答えていけば，この議論は深まり，よりよい方法が見出されていくに違いない。 　これに対し，「成功させる必要はない。なぜなら，まずはイベントをおこなうということが大事なのだから」と主張するなら，それは反論ではなく，「異論」を提出しているわけである。つまり，「ＡだからＢ」と主張している人に，「Ａだからと言ってＢとは言えない」というように論証の部分に批判を加えることが反論であり，反論であるからには，相手の述べたＡやＢを問題にして，「そうではない」ということの理由を付して論じる（つまり，論証する）必要がある。その結果，反論に説得力があれば，相手の主張Ｂを退けることになるのが反論である。しかし，「Ｂでない。なぜならＣだから」と相手が述べていないことを持ち出して，自説を展開することは異論である。その違いにまず気をつけてほしい。 〇論証のどこに目をつけるか 　では例をとりあげて考えていこう。新聞に次のような投書が掲載されていたとしよう。それを読んだあなたはどうも賛成できない。反論の投書を出すとしたら，どの点に反論するだろうか。 　近年，高校中退者が激増していると聞く。一念発起し高卒認定試験を受けて進学する者もいるが，多くはそのままフリーターとなりちゃんとした職業に就かない。これではよくないからと「高校中退者を救う会」なるものが結成されたそうだ。中退者の相談にのリ，復学を勧めたリ勉強を続けられるよう支援をしたりするという。 　しかし，そのような会が必要だろうか。現在の高校教育が十分なものでないということは理解している。とはいえ，ほとんどの高校生はきちんと高校を卒業しそれぞれの進路を選び取っている。中退者はおおむね，高校が悪い，先生が悪いと責任転嫁をし，自ら努力をしなかった結果そうなっている。いわば自分のせいで中退することになったのである。そうした者を守り救うなどといったことは過保護である。自分の責任は自分で取らせるべきである。 　「中退者がフリーターになるとはかぎらない」とか，「人のせいにして中退する者ばかりではない」といった反論がすぐに思い浮かぶだろう。それはまったくもっともである。しかし，ポイントはそこにはない。事実認識を争っても，反論としては効果的ではない。ともかくすべきはまず，論証を取り出すことである。 〇反論のポイント 　投書者の主張は何か。「中退者を救う会は必要ない」，すなわち「中退者を救う必要はない」ということである。では，その根拠は何か。「自分のせいで中退しているから」ということである。 　前提：中退者は自分のせいで中退している。 　結論：中退者を救う必要はない。 　注目すべきは，前提からどのようにして結論が出てきているのかということである。この2つの前提だけでは結論は出てこない。この論証を補う前提は何か。この論証はよくみると「ＡはＢである。ゆえにＡはＣである」という形をしている。前提と結論を媒介する隠れた前提は「ＢはＣだ」，すなわち「自分のせいで中退している者を救う必要はない」である。 　まず論証の形を取り出し，論証者が暗黙のうちに前提している事柄をはっきりさせる。そしてその前提が適切かを問うことが必要である。「自分のせいで中退した者を救う必要はない」と考えるのは，「自分のせいで生じた結果を他人が救ってやる必要はない」というさらに一般化された前提を採用しているからである。この一般的な前提は，もはや事実問題ではなく，論証者の考えの表明である。この前提を問題にすべきである。「自業自得で一定の状態になった人を救う必要はない」のか。 　一概にそうは言えないことは明らかだろう。「Ａだ」という主張に反論するためには，「Ａだ，ということはない」と論証できればよい。無条件に「Ａだ」とする主張には，「一概にＡだとは言えない。Ａであるときもあれば，Ａでないときもある」と言えれば十分である。この点については後述する。 　この投書者に対しては，たとえば，「中退者を救う必要がないと考えるのは，自分のせいで陥った状態からその人を救ってやる必要はないということを投書者が前提しているからだ。しかし，そうした前提は常に正しいわけではない。その前提をとるなら，自分の不注意から川でおぼれている人がいるとき，自分のせいなのだからその人を救う必要はない，ということになってしまう。投書者が暗黙のうちに前提していることはケースによるのであり，無条件に前提できることではない」と述べれば効果的な反論となるだろう。

論理的思考の技法（1）第2版 「ならば」をめぐって [ 鈴木美佐子 ] 価格：1650円（税込、送料無料) (2020/1/23時点) 楽天で購入